Trainer Fishr¶
Invariant Gradient Variances for Out-of-distribution Generalization¶
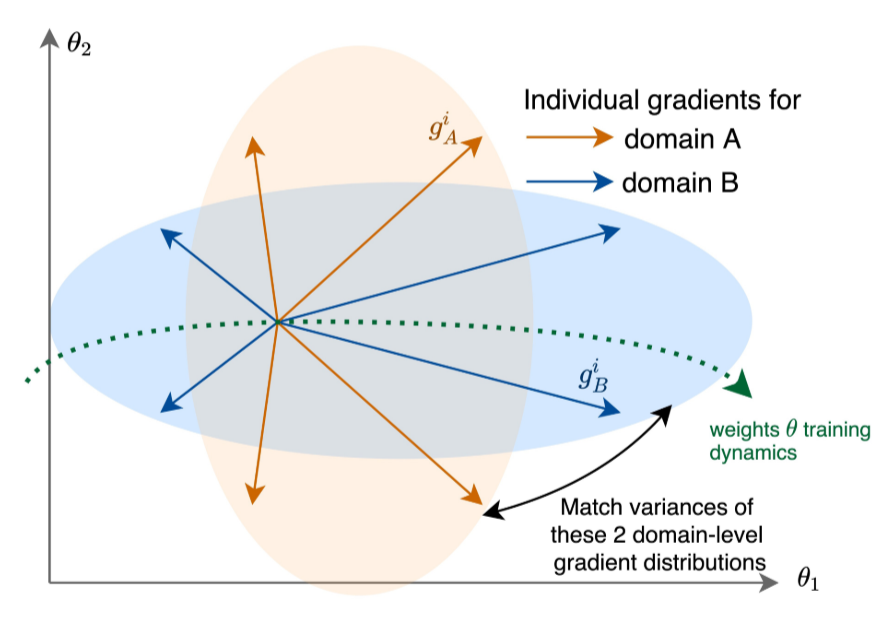
The goal of the Fishr regularization technique is locally aligning the domain-level loss landscapes around the final weights, finding a minimizer around which the inconsistencies between the domain-level loss landscapes are as small as possible. This is done by considering second order terms during training, matching the variances between the domain-level gradients.
Quantifying inconsistency between domains¶
Intuitively, two domains are locally inconsistent around a minimizer, if a small perturbation of the minimizer highly affects its optimality in one domain, but only minimally affects its optimality in the other domain. Under certain assumptions, most importantly the Hessians being positive definite, it is possible to measure the inconsistency between two domains \(A\) and \(B\) with the following inconsistency score:
, whereby \(\theta^*\) denotes the minimizer, \(\mathcal{E}\) denotes the set of training domains, \(H_e\) denotes the Hessian for \(e\in\mathcal{E}\), \(\theta\) denote the network parameters and \(\mathcal{R}_e\) for \(e\in\mathcal{E}\) denotes the domain-level ERM objective. The Fishr regularization method forces both terms on the right hand side of the inconsistency score to become small. The first term represents the difference between the domain-level risks and is implicitly forced to be small by applying the Fishr regularization. For the second term it suffices to align diagonal approximations of the domain-level Hessians, matching the variances across domains.
Matching the Variances during training¶
Let \(\mathcal{E}\) be the space of all training domains, and let \(\mathcal{R}_e(\theta)\) be the ERM objective. Fishr minimizes the following objective function during training:
, whereby
with \(v_e\) denoting the variance between the gradients of domain \(e\in\mathcal{E}\) and \(v\) denoting the average variance of the gradients across all domains, i.e. \(v = \frac{1}{|\mathcal{E}|}\sum_{e\in\mathcal{E}} v_e\).
Implementation¶
The variance of the gradients within each domain can be computed with the BACKPACK package (see: Dangel, Felix, Frederik Kunstner, and Philipp Hennig. “Backpack: Packing more into backprop.” https://arxiv.org/abs/1912.10985). Further on, we use \( \textnormal{Var}(G) \approx \textnormal{diag}(H) \). The Hessian is then approximated by the Fisher Information Matrix, which again is approximated by an empirical estimator for computational efficiency. For more details, see the reference below or the domainlab code.
Examples¶
python main_out.py --te_d=0 --task=mini_vlcs --model=erm --trainer=fishr --nname=alexnet --bs=2 --nocu
Reference: Rame, Alexandre, Corentin Dancette, and Matthieu Cord. “Fishr: Invariant gradient variances for out-of-distribution generalization.” International Conference on Machine Learning. PMLR, 2022.